F Critical Value: Definition, formula, and Calculations

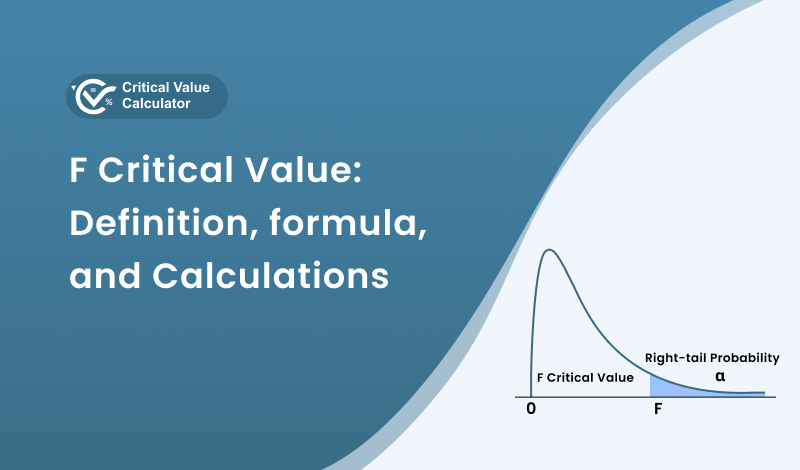
Critical values are like cut-off scores that help us decide whether the findings of a study are something special or just due to chance. In statistics, when we want to see if different groups are really different from each other, we use something called an F critical value. This special number comes from a bell-shaped curve that's squished to one side, known as the F-distribution.

Let’s learn more about this critical value.

Definition:

The F-distribution is a continuous probability distribution that arises frequently as the null distribution of a test statistic under the null hypothesis. It is asymmetric and only defined for positive values. 

F-statistics is a threshold derived from the F-distribution that is used to determine whether to reject the null hypothesis in the context of hypothesis testing. When you perform a statistical test that uses the F-distribution, such as an ANOVA, you compare the calculated F-statistic from your data to the F-critical value.

The F critical value depends on two key factors:

The Significance Level (α): This is the probability of rejecting the null hypothesis when it is actually true, typically set at 0.05, 0.01, or 0.10.

Degrees of Freedom: These are determined by the sample size and the number of groups or categories you are comparing. The F-distribution has two sets of degrees of freedom: the numerator degrees of freedom (df₁) and the denominator degrees of freedom (df₂), which correspond to the variance estimates between groups and within groups, respectively.

Formula:

The general formula for an F-statistic is:

\[F = \frac{\text{MSB}}{\text{MSW}}\]

Where:

• MSB is the Mean Square Between groups (variance due to the interaction between the groups).
• MSW is the Mean Square Within groups (variance within each group).

But for the F critical value, which is the value you compare your F-statistic to, there isn't a direct formula like this because it's obtained from an F-distribution table or calculated using statistical software, which takes into account the degrees of freedom for the numerator and the denominator, as well as the significance level (alpha).

Interpreting the F-critical value:

Interpreting the F-critical value involves comparing it to the calculated F statistic from your data analysis. Here's how to interpret the F critical value in the context of hypothesis testing, such as ANOVA:

• If your F statistic is greater than the F critical value, this suggests that the variance between the groups is significantly larger than the variance within the groups. In other words, there is a statistically significant difference between group means. You would reject the null hypothesis, which typically states that there is no difference.
• If your F statistic is less than or equal to the F critical value, there isn't enough evidence to say that the group variances are significantly different from each other. You would fail to reject the null hypothesis, meaning that any observed differences could likely be due to chance.

How to calculate the F-critical value?

To find the F critical value for a statistical test such as ANOVA, you'll typically follow these steps, assuming you don't have software that can compute it for you:

• Determine the Degrees of Freedom. The numerator degrees of freedom (df₁) is the number of groups minus one. The denominator degrees of freedom (df₂) is the total number of observations minus the number of groups.
• Choose a Significance Level (α).
• Use an F-Distribution Table: With your degrees of freedom and significance level, use an F-distribution table, which you can find in many statistics textbooks or online. Here's how to use it: 

Find the row that corresponds to your numerator degrees of freedom (df₁). 

Find the column that corresponds to your denominator degrees of freedom (df₂). Cross-reference the row and column based on your chosen significance level to find the F critical value.

• Using Software or an Online Calculator: Input your degrees of freedom (df₁ and df₂) and the significance level (α) into the software to get the F critical value. Common statistical software packages like R, Python’s SciPy library, or online F-distribution calculators can compute the F critical value for you.

Solved example:

Let’s go through an example of calculating the F-statistic for a one-way ANOVA by hand.

Imagine a teacher who wants to determine if three different teaching methods have different effects on students' test scores. She divides her class into three groups, each receiving a different teaching method. After a month, a test is given to all groups. Here are the test scores:

Group 1 (Method A): 80, 85, 83, 90

Group 2 (Method B): 78, 74, 75, 76

Group 3 (Method C): 90, 92, 93, 94

Steps for ANOVA:

1. Calculate the overall mean (Grand Mean, GM):

\[GM = \frac{\sum \text{all scores}}{\text{Total no. of scores}}\]

2. Calculate the sum of squares between groups (SSB), which reflects how much each group mean deviates from the grand mean:

\[SSB = \sum_{i=1}^{k} n_i (\bar{X}_i - GM)^2\]

Where n_i is the number of observations in the group "i", x̄_i  is the mean of the group "i", and GM is the grand mean.

3. Calculate the sum of squares within groups (SSW), which captures the variability within each group:

\[SSW = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (X_{ij} - \bar{X}_i)^2\]

Where X_ij is the jth score in the ith group and x̄_i is the mean of the group "i".

4. Calculate the Mean Square Between (MSB) and the Mean Square Within (MSW):

\[MSB = \frac{SSB}{df_{between}}\]

\[MSW = \frac{SSW}{df_{within}}\]

Where df_between is the degrees of freedom between groups (k-1) and df_within  is the degrees of freedom within groups (N - k)

5. Calculate the F-statistic:

\[F = \frac{MSB}{MSW}\]

Let’s do the calculations:

1. Overall mean:

\[GM = \frac{80 + 85 + 83 + 90 + 78 + 74 + 75 + 76 + 90 + 92 + 93 + 94}{12}\]

\[GM = \frac{1000}{12}\]

\[GM = 83.33\]

2. Means for each group:

For x̄₁

\[\bar{X}_1 = \frac{80 + 85 + 83 + 90}{4}\] 

\[\bar{X}_1 = \frac{338}{4}\] 

\[\bar{X}_1 = 84.5\]

For x̄₂

\[\bar{X}_2 = \frac{78 + 74 + 75 + 76}{4}\]

\[\bar{X}_2 = \frac{303}{4}\]

\[\bar{X}_2 = 75.75\]

For x̄₃

\[\bar{X}_3 = \frac{90 + 92 + 93 + 94}{4}\]

\[\bar{X}_3 = \frac{369}{4}\] 

\[\bar{X}_3 = 92.25\]

3. SSB:

\[SSB = 4(84.5 - 83.33)^2 + 4(75.75 - 83.33)^2 + 4(92.25 - 83.33)^2\]

\[SSB = 4(1.17)^2 + 4(-7.58)^2 + 4(8.92)^2\]

\[SSB = 4(1.37) + 4(57.47) + 4(79.57)\]

\[SSB = 5.48 + 229.88 + 318.2\]

\[SSB = 553.64\]

4. SSW:

For each score X_ij, subtract the group means x̄_i and square the result. Then sum all those squares within each group.

\[SSW = \sum (X_{1j} - \bar{X}_1)^2 + \sum (X_{2j} - \bar{X}_2)^2 + \sum (X_{3j} - \bar{X}_3)^2\]

\[SSW = (-4.5)^2 + (0.5)^2 + (-1.5)^2 + (5.5)^2 + (2.25)^2 + (-1.75)^2 + (-0.75)^2 + (0.25)^2 + (-2.25)^2 + (-0.25)^2 + (0.75)^2 + (1.75)^2\]

\[SSW = 20.25 + 0.25 + 2.25 + 30.25 + 5.0625 + 3.0625 + 0.5625 + 0.0625 + 5.0625 + 0.0625 + 0.5625 + 3.0625\]

\[SSW = 71.0625\]

5. Degrees of freedom:

\[df_{between} = 3 - 1 = 2\]

\[df_{within} = 12 - 3 = 9\]

6. Mean Squares:

\[MSB = \frac{SSB}{df_{between}} = \frac{553.64}{2} = 276.82\]

\[MSW  = \frac{SSW}{df_{within}} = \frac{100}{9} \approx 11.11\]

7. F-Statistics:

\[F = \frac{MSB}{MSW} = \frac{276.82}{11.11} \approx 24.92\]

8. Compare with table:

With a calculated F-statistic of 24.92, degrees of freedom for the numerator (df₁) as 2, and degrees of freedom for the denominator (df₂) as 9, we will now compare this to the F-distribution critical values table at the 0.05 significance level.

Please note, that the following values are based on a standard F-distribution table:

For this data, the critical value of F at the 0.05 significance level might be approximately 4.26.

Since our calculated F-statistic (24.92) is much higher than the critical value from the table (approximately 4.26), we would reject the null hypothesis. This indicates that there is a statistically significant difference between the means of the groups being tested at the 0.05 significance level.

F- Distribution Table:

| df₁\df₂|  1   |  2   |  3   |  4   |  5   |  6   |  7   |  8   |  9   |  10  |

---------------------------------------------------------------------------------

|  1      | 161.4| 199.5| 215.7| 224.6| 230.2| 233.9| 236.8| 238.9| 240.5| 241.9|

|  2      | 18.51| 19.00| 19.16| 19.25| 19.30| 19.33| 19.35| 19.37| 19.38| 19.39|

|  3      | 10.13|  9.55|  9.28|  9.12|  9.01|  8.94|  8.89|  8.85|  8.81|  8.79|

---------------------------------------------------------------------------------

| df₁\df₂|  11  |  12  |  13  |  14  |  15  |  16  |  17  |  18  |  19  |  20  |

---------------------------------------------------------------------------------

|  1      | 243.1| 243.9| 244.6| 245.2| 245.7| 246.2| 246.6| 246.9| 247.2| 247.4|

|  2      | 19.40| 19.41| 19.42| 19.43| 19.44| 19.44| 19.45| 19.45| 19.46| 19.46|

|  3      |  8.76|  8.74|  8.73|  8.71|  8.70|  8.69|  8.68|  8.67|  8.66|  8.66|

-------------------------

Conclusion:

To wrap up the article on F critical values, we can say that the F critical value is a key figure in the ANOVA test. It helps us decide whether the differences between group means are statistically significant.