Critical Value Calculator

What is a critical value?

A critical value is a point on the t-distribution that is compared to the test statistic to determine whether to reject the null hypothesis in hypothesis testing. If the absolute value of the test statistic is greater than the critical value, statistical significance can be declared as well as the null hypothesis can be rejected.

Critical value tests can be:

Left-tailed test: Q (α)

---

Right-tailed test: Q (1 - α)

---

Two-tailed test: Q (α/2)] ∪ Q (1 - α/2)

---

What is a t critical value?

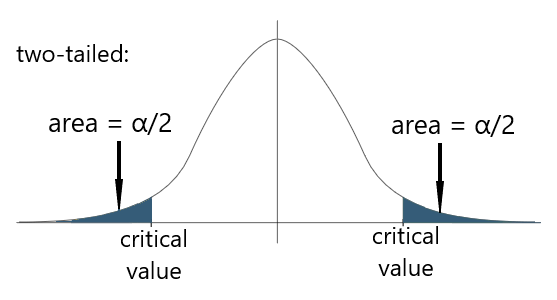
T critical value is a point that cuts off the student t distribution. T value is used in a hypothesis test to compare against a calculated t score. The critical value of t helps to decide if a null hypothesis should be supported or rejected.

What is a z critical value?

Z critical value is a point that cuts off an area under the standard normal distribution. The critical value of z can tell what probability any particular variable will have.
Z and t critical values are almost identical.

What is f critical value?

F critical value is a value at which the threshold probability α of type-I error (reject a true null hypothesis mistakenly).  The f statistics is the value that follows the f-distribution table.

Here are a few tests that help to calculate the f values.

• ANOVA
• Overall significance in regression analysis. k
• Compare two nested regression models. 
• The equality of variances in two normally distributed populations.

All the above tests are right-tailed. F critical value calculator above will help you to calculate the f critical value with a single click.

What is the chi-square value?

In certain hypothesis tests and confidence intervals, chi-square values are thresholds for statistical significance. The Chi-square distribution table is used to evaluate the chi-square critical values. It is rather tough to calculate the critical value by hand, so try a reference table or chi-square critical value calculator above.

The chi-square critical values are always positive and can be used in the following tests.

• Goodness-of-fit tests
• Homogeneity tests
• Tests for independence in contingency tables

Unlike the t & f critical value, Χ² (chi-square) critical value needs to supply the degrees of freedom to get the result.

Critical value formula

The formula of z and t critical value can be expressed as:

Where,

• Q_t is the quantile function of t student distribution
• u is the quantile function of the normal distribution
• d refers to the degree of freedom
• α is the significance level

A critical value of t calculator uses all these formulas to produce the exact critical values needed to accept or reject a hypothesis.

How to find critical values?

Calculating critical value is a tiring task because it involves looking for values into the t-distribution chart. The t-distribution table (student t-test distribution) consists of hundreds of values, so, it is convenient to use t table value calculator above for critical values.
However, if you want to find critical values without using t table calculator, follow the examples given below.

How to find t critical value?

Example:

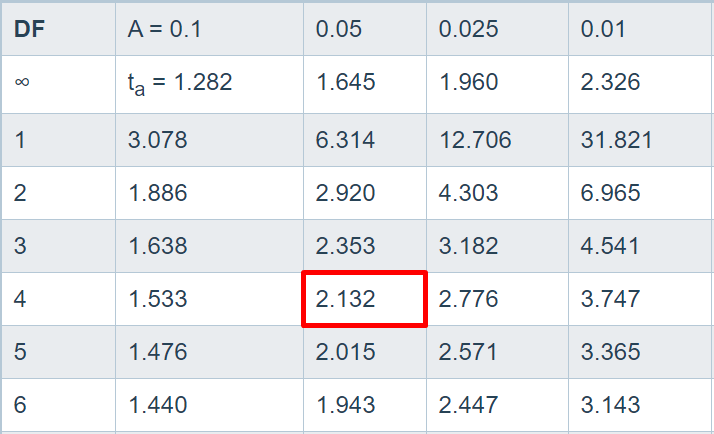
Find the t critical value if the size of the sample is 5 and the significance level is 0.05.

Solution:

Step 1:

Subtract 1 from the sample size to get the degree of freedom.
Degree of Freedom = N – 1 = 5 – 1
Degree of freedom = 4
α = 0.05

Step 2:

Depending on the test, choose the one-tailed t distribution table or two-tailed t table below.

Step 3:

Look for the degree of freedom in the most left column. Also, look for the significance level α in the top row. Pick the value occurring at the intersection of the mentioned row and column.
In this case, the t critical value is 2.132.

How to find z critical value?

Example:

Find the z critical value if the significance level is 0.02.

Solution:

Step 1:

Divide the significance level α by 2
α/2 = 0.02/2
α/2 = 0.01

Step 2:

Subtract α/2 from 1.
1 - α/2 = 1 – 0.01
1 - α/2 = 0.99

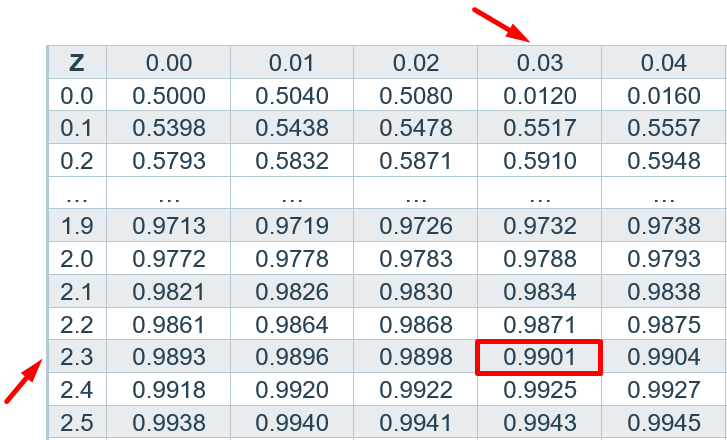
Step 3:

Search the value 0.99 in the z table given below. Add the values of intersecting row (top) and column (most left) to get the z critical value.
2.3 + 0.03 = 2.33
Z critical value = ±2.33 for the two-tailed test.

T-Distribution Table (One Tail)

The t table for one-tail probability is given below.

Download Table

T-Distribution Table (Two Tail)

The t table for two-tail probability is given below.

Download Table

Z table (right-tailed)

The normal distribution table for the right-tailed test is given below.

Download Table

Z table (left-tailed)

The normal distribution table for the left-tailed test is given below.

Download Table