To find the variance using the variance calculator, follow the below steps:
Give Feedback What do you think of variance calculator?
Worst
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
Variance calculator finds the variance of sample and population data values with steps. The sample variance calculator also provides the standard deviation, mean, and sum of squares.
In statistics, the variance is the measure of dispersion i.e., measure the spread of data values from the expected value. It is the expectation of the squared deviation of a random variable from its sample or population mean.
It is denoted by s2 and σ2 for sample and population data respectively.
The formula for the sample variance is:
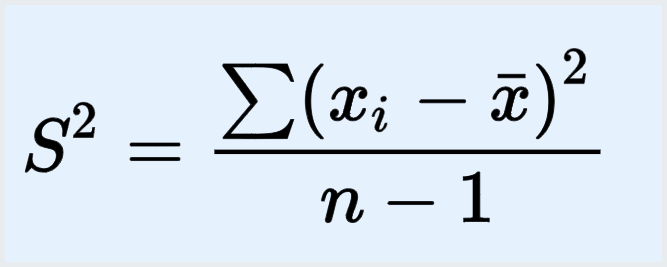
The formula for the population variance is:
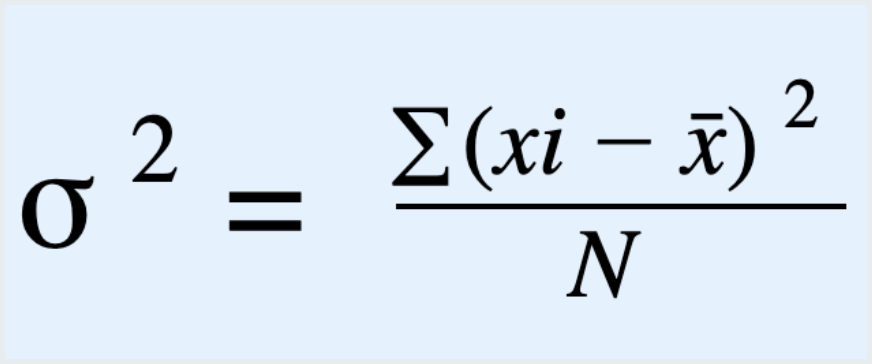
Below are a few examples of variance solved by our mean and variance calculator.
Example 1: For sample variance
Find the variance of the given sample data.
2, 4, 7, 12, 15
Solution
Step 1: Calculate the sample mean of the given data.
Sample mean = x̅ = Σx/n
Sample mean = x̅ = [2 + 4 + 7 + 12 + 15]/5
Mean = x̅ = 40/5
Mean = x̅ = 8
Step 2: Now measure the dispersion and squares of deviation.
| Data values (x) | xi - x̅ | (xi - x̅)2 |
| 2 | 2 – 8 = -6 | (-6)2 = 36 |
| 4 | 4 – 8 = -4 | (-4)2 = 16 |
| 7 | 7 – 8 = -1 | (-1)2 = 1 |
| 12 | 12 – 8 = 4 | (4)2 = 16 |
| 15 | 15 – 8 = 7 | (7)2 = 49 |
Step 3: Find the summation of the squared deviations.
Σ(xi - x̅)2 = 36 + 16 + 1 + 16 + 49
Σ(xi - x̅)2 = 118
Step 4: Now divide the sum of squares by n-1.
Σ(xi - x̅)2/n-1 = 118/5-1
Σ(xi - x̅)2 / n-1 = 118/4
Σ(xi - x̅)2 / n-1 = 29.5
Example 2: For population variance
Find the variance of the given population data.
1, 14, 19, 25, 26, 35
Solution
Step 1: Calculate the population mean of the given data.
Population mean = µ = Σx/n
= [1 + 14 + 19 + 25 + 26 + 35]/6
= 120/6
= 20
Step 2: Now measure the dispersion and squares of deviation.
Data values (x) | xi - µ | (xi - µ)2 |
1 | 1 – 20 = -19 | (-19)2 = 361 |
14 | 14 – 20 = -6 | (-6)2 = 36 |
19 | 19 – 20 = 1 | (1)2 = 1 |
25 | 25 – 20 = 5 | (5)2 = 25 |
26 | 26 – 20 = 6 | (6)2 = 36 |
35 | 35 – 20 = 15 | (15)2 = 225 |
Step 3: Find the summation of the squared deviations.
Σ(xi - µ)2 = 361 + 36 + 1 + 25 + 36 + 225
Σ(xi - µ)2 = 684
Step 4: Now divide the sum of squares by n.
Σ(xi - µ)2/n = 684/6
Σ(xi - µ)2/n = 136.8
How to find population variance?
To calculate the population variance, you can use the formula:
Where:
· 
𝑁: The size of the population
· 𝜇: The population mean
Wikimedia Foundation. (2022, June 20). What is a variance? Wikipedia.
Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.
