Covariance Calculator

The covariance calculator is designed to find the covariance for two data sets and the values related to it e.g

• Mean of X
• Mean of Y
• Population covariance
• Sample covariance
• No. of inputs

Users can find the covariance in the form of a covariance matrix through this calculator as well.

What is covariance?

Covariance is a technique to measure the relationship of bivariate data values. In simple words, it tells the extent to which two different variables are dependent on each other.

Covariance also explains the behavior of one variable, when the other changes. Covariance can only tell the direction of the relationship whereas the strength of this relationship is computed using correlation. 

There are three types of covariance.

Negative covariance:

Negative covariance is indicated with the (-) minus sign with the covariance value. It tells that variables are related in an indirect manner. 

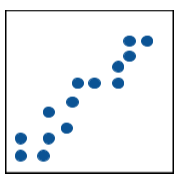
If variable A increases, then due to the negative covariance, variable B will decrease.

Positive covariance:

Positive covariance is indicated with the (+) plus sign with the covariance value. It tells that variables are related in a direct manner. 

If variable A increases, then due to the positive covariance, variable B will also increase.

Zero covariance:

Zero covariance is indicated with 0 numeric digit or the values very closely surrounding it.

It tells that when variable A increases, no significant change is seen in variable B. 

Covariance is from the family of correlation and both are closely related. Similarly, variance and covariance are interrelated. Covariance is bivariate while variance is univariate. Both measure variability. 

Covariance formula:

There are two types of covariance formulas. Sample covariance and population covariance.

For population:

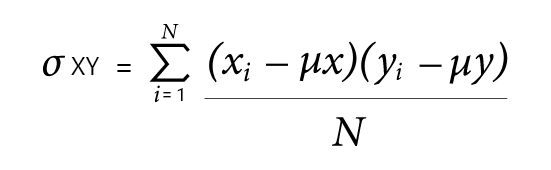
Where:
σ_XY = Population covariance of X and Y.
μx = population mean of X.
μy = population mean of Y.

For example:

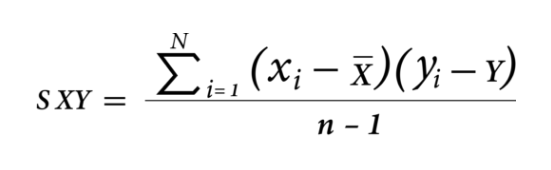
In this formula:
sXY = sample covariance of X and Y
 ͞x = Sample mean of X 
 ͞y = sample mean of y

How to calculate covariance?

If you face any problem while finding covariance, you can use the sample covariance calculator above. It gives the values computed at each step. This way you can verify your solution and identify the problem.

To find the covariance by hand, follow these steps. 

1. Find the mean of X
2. Find the means of Y.
3. Subtract each x value from the mean of x.
4. Similarly, subtract each y value from the mean of y.  
5. Multiply with the corresponding value.
6. Find the sum of these values. 
7. Divide by the n-1.

Example:

For this random dataset, find the covariance.

Solution:
Step 1: Find the means.

Mean of X = 12 + 17 + 10 + 15 + 11 + 20 + 13 + 19 + 18 + 19 / 10
                  = 154 / 10
                  = 15.4

Mean of Y = 28 + 28 + 10 + 35 + 24 + 40 + 20 + 18 + 18 + 21 / 10
                 = 242 / 10
                 = 24.2

Step 2: Subtract the values of x and y from their means and multiply.

Step 3: Add these values.
=  -12.92 + 6.08 + 76.68 + (-4.32) + 0.88 + 72.68 + 10.08 + (-22.32) + (-16.12) + (-11.52) 
= 99.20

Step 4: Put this number in the Covariance formula.

Cov(x, y) = ∑ (xi - ͞x ) (yi -͞y ) / n-1  
               = 99.20 / 10 -1 
               = 99.20 / 9
               = 11.02

The number itself is not important. Only the sign is vital. Since the result is a positive value, the covariance is also positive.