The working principle of the margin of error calculator is very easy;
Give Feedback What do you think of margin of error calculator?
Worst
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
The margin of error calculates the MOE using sample size (n), population size (P), sample proportion (p), and confidence level. It gives a step-by-step solution to the problem.
The margin of error (MOE) for a survey tells you ways close you'll be able to expect the survey results to be to the proper population price. E.g., In a random survey, we came to know that 55% of the population favored Brand X over Brand Y with 2% MOE.
According to this survey, the actual population percentage that voted for Brand X falls within the range of 55% ± 2%. MOE refers to the degree of error in the results that we get from surveys of random sampling.
There are two different cases to calculate the margin of error of a raw sample.
The formula to calculate the MOE with FPC is as follows:
MOE with finite population correction :
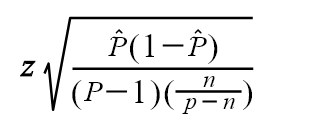
Now let’s have a look at the FPC, in the sample survey statistics, this concept plays a vital role. It is a factor that is used to balance the estimated variance for a hypothetical total or mean.
In the above formula,
The simple MOE can be calculated using the following formula:
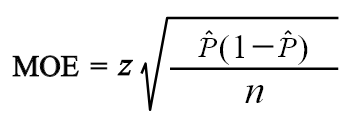
In this section, with the assistance of examples, the procedure is explained briefly.
Example 1:
Calculate the MOE with FPC if the sample proportion is 0.2, the population size is 1029, the sample size is 112, and the confidence interval is 95%.
Solution:
Step 1: Extract the data
Sample proportion = = 0.2
Population size = p = 1029
The confidence interval of z at 95% = 1.960
Sample size = n = 112
Step 2: enter the values in the following formula
MOE with FPC =
MOE with FPC = 1.960 {{0.2 (1 - 0.2)}/ {112(1029 – 1)/ (1029 – 112)}
MOE with FPC = 1.960 {0.2 (0.8) / {(112) * (1028) / (917)}}}
MOE with FPC = 1.960 { 0.2(0.8)/ {112(1.121)}
MOE with FPC = 1.960 {0.16/ {125.55}}
MOE with FPC = 1.960 * 0.03569761
MOE with FPC = 0.06996
MOE with FPC = 6.997%
Margin of error | Statistics How To.
Your guide to margin of error | Qualtrics.
Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.
