Decile Calculator

Decile calculator:

The decile calculator with solution calculates the deciles (1^st to 10^th) of the entered data set it also calculates the minimum value, maximum value, mean, sum, and range of the given input.

What are deciles?

In statistics, deciles are a measure of position that divides a dataset into 10 equal parts, each containing an equal number of observations.

Specifically, the k^th decile is the value below which k/10 of the observations in the dataset fall, and above which (10 - k) / 10 of the observations fall. It is quite similar to quartiles. 

• The first decile (10th percentile) is the value below which 10% of the observations in the dataset fall
• The second decile (20th percentile) is the value below which 20% of the observations fall.
• The fifth decile (50th percentile) is the value below which 50% of the observations fall, which is also known as the median.

Formulas for calculating the deciles of a data set:

To calculate the decile of a data set we use the following decile formula:

• “K” is the number of deciles it can be between 1 to 10
• “n” is the number of terms

Example section:

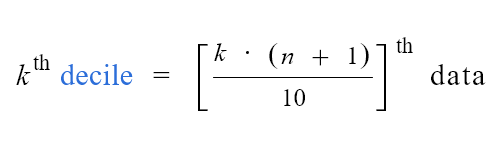
In this section, we’ll discuss the steps for calculating the deciles of any data set.

Example 1:

Calculate the deciles of the following data set:

2, 23, 4, 91, 5, 6, 3, 76, 83, 32

Solution:

Step 1: Arrange the data

Firstly we have to arrange the data in ascending order.

X = 2, 3, 4, 5, 6, 23, 32, 76, 83, 91

Step 2: Calculate “n”.

Total number of terms = n = 10

Step 3: Calculation.

Calculate the deciles using the formula:

K^th decile = [{k * (n + 1)} / 10]^th data

For 1^st decile:

K = 1

n = 10

K^th decile = [{k * (n + 1)} / 10]^th data

1^st decile = [{1 * (10 + 1)} / 10]^th data

1^st decile = [{1 * (11)} / 10]^th data

1^st decile = [11 / 10]^th data

1^st decile = [1.1]^th data

1^st decile = 1^st term + (0.1) ^th data

1^st decile = 2 + (0.1) ^th data

For “(0.1)^th data” subtract 1^st term from the 2^nd term, and then multiply it by “0.1”

1^st decile = 2 + {(2^nd term – 1^st term) * 0.1}

1^st decile = 2 + {(3 – 2) * 0.1}

1^st decile = 2 + {(1) * 0.1}

1^st decile = 2 + 0.1

1^st decile = 2.1

For 2^nd decile:

K = 2

n = 10

2^nd decile = [{2 * (10 + 1)} / 10]^th data

2^nd decile = [{2 * (11)} / 10]^th data

2^nd decile = [22 / 10]^th data

2^nd decile = [2.2]^th data

2^nd decile = 2^nd term + (0.2) ^th data

2^nd decile = 3 + (0.2) ^th data

For “(0.2) ^th data” subtract 2^nd term from the 3^rd term, and then multiply it by “0.2”

2^nd decile = 3 + {(3^rd term – 2^nd term) * 0.2}

2^nd decile = 3 + {(4 – 3) * 0.2}

2^nd decile = 3 + {(1) * 0.2}

2^nd decile = 3 + 0.2

2^nd decile = 3.2

For 3^rd decile:

K = 3

n = 10

3^rd decile = [{3 * (10 + 1)} / 10]^th data

3^rd decile = [{3 * (11)} / 10]^th data

3^rd decile = [33 / 10]^th data

3^rd decile = [3.3]^th data

3^rd decile = 3^rd term + (0.3) ^th data

3^rd decile = 4 + (0.3) ^th data

For “(0.3) ^th data” subtract 3^rd term from the 4^th term, and then multiply it by “0.3”

3^rd decile = 4 + {(4^th term – 3^rd term) * 0.3}

3^rd decile = 4 + {(5 – 4) * 0.3}

3^rd decile = 4 + {(1) * 0.3}

3^rd decile = 4 + 0.3

3^rd decile = 4.3

For 4^th decile:

K = 4

n = 10

4^th decile = [{4 * (10 + 1)} / 10]^th data

4^th decile = [{4 * (11)} / 10]^th data

4^th decile = [44 / 10]^th data

4^th decile = [4.4]^th data

4^th decile = 4^th term + (0.4) ^th data

4^th decile = 5 + (0.4) ^th data

For “(0.4) ^th data” subtract 4^th term from the 5^th term, and then multiply it by “0.4”

4^th decile = 5 + {(5^th term – 4^th term) * 0.4}

4^th decile = 5 + {(6 – 5) * 0.4}

4^th decile = 5 + {(1) * 0.4}

4^th decile = 5 + 0.4

4^th decile = 5.4

For 5^th decile:

K = 5

n = 10

5^th decile = [{5 * (10 + 1)} / 10]^th data

5^th decile = [{5 * (11)} / 10]^th data

5^th decile = [55 / 10]^th data

5^th decile = [5.5]^th data

5^th decile = 5^th term + (0.5) ^th data

5^th decile = 6 + (0.5) ^th data

For “(0.5) ^th data” subtract 5^th term from the 6^th term, and then multiply it by “0.5”

5^th decile = 6 + {(6^th term – 5^th term) * 0.5}

5^th decile = 6 + {(23 – 6) * 0.5}

5^th decile = 6 + {(17) * 0.5}

5^th decile = 6 + 8.5

5^th decile = 14.5

For 6^th decile:

K = 6

n = 10

6^th decile = [{6 * (10 + 1)} / 10]^th data

6^th decile = [{6 * (11)} / 10]^th data

6^th decile = [66 / 10]^th data

6^th decile = [6.6]^th data

6^th decile = 6^th term + (0.6) ^th data

6^th decile = 23 + (0.6) ^th data

For “(0.6) ^th data” subtract 7^th term from the 6^th term, and then multiply it by “0.6”

6^th decile = 23 + {(7^th term – 6^th term) * 0.6}

6^th decile = 23 + {(32 – 23) * 0.6}

6^th decile = 23 + {(9) * 0.6}

6^th decile = 23 + 5.4

6^th decile = 28.4

For 7^th decile:

K = 7

n = 10

7^th decile = [{7 * (10 + 1)} / 10]^th data

7^th decile = [{7 * (11)} / 10]^th data

7^th decile = [77 / 10]^th data

7^th decile = [7.7]^th data

7^th decile = 7^th term + (0.7) ^th data

7^th decile = 32 + (0.7) ^th data

For “(0.7) ^th data” subtract 7^th term from the 8^th term, and then multiply it by “0.7”

7^th decile = 32 + {(7^th term – 6^th term) * 0.7}

7^th decile = 32 + {(76 – 32) * 0.7}

7^th decile = 32 + {(44) * 0.7}

7^th decile = 32 + 30.8

7^th decile = 62.8

For 8^th decile:

K = 8

n = 10

8^th decile = [{8 * (10 + 1)} / 10]^th data

8^th decile = [{8 * (11)} / 10]^th data

8^th decile = [88 / 10]^th data

8^th decile = [8.8]^th data

8^th decile = 8^th term + (0.8) ^th data

8^th decile = 76 + (0.8) ^th data

For “(0.8) ^th data” subtract 8^th term from the 9^th term, and then multiply it by “0.8”

8^th decile = 76 + {(9^th term – 8^th term) * 0.8}

8^th decile = 76 + {(83 – 76) * 0.8}

8^th decile = 76 + {(7) * 0.8}

8^th decile = 76 + 5.6

8^th decile = 81.6

For 9^th decile:

K = 9

n = 10

9^th decile = [{9 * (10 + 1)} / 10]^th data

9^th decile = [{9 * (11)} / 10]^th data

9^th decile = [99 / 10]^th data

9^th decile = [9.9]^th data

9^th decile = 9^th term + (0.9) ^th data

9^th decile = 83 + (0.9) ^th data

For “(0.9) ^th data” subtract 9^th term from the 10^th term, and then multiply it by “0.9”

9^th decile = 83 + {(10^th term – 9^th term) * 0.9}

9^th decile = 83 + {(91 – 83) * 0.9}

9^th decile = 83 + {(8) * 0.9}

9^th decile = 83 + 7.2

9^th decile = 90.2

For 10^th decile:

The maximum term of the data set is the 10^th decile, so:

10^th decile = 91

References:

What are Deciles | Study.com

Formula of decile | WallStreetMojo