To calculate the probability of any data using hypergeometric distribution calculator, follow the below steps:
Give Feedback What do you think of hypergeometric distribution calculator?
Worst
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
The Hypergeometric distribution calculator is used to calculate the probability of a raw data, it also calculates mean, standard deviation, and variance of the entered data according to the properties of Hypergeometric distribution.
Generally, in statistics and probability theory, the hypergeometric distribution refers to a discrete probability distribution of success.
To calculate the probability of success using Hypergeometric distribution, we use the following formula:
There are three properties of the hypergeometric distribution
The mean of the hypergeometric distribution can be calculated by using the following formula:
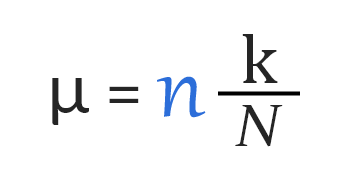
Standard deviation is a property of the hypergeometric distribution, it can be calculated as:
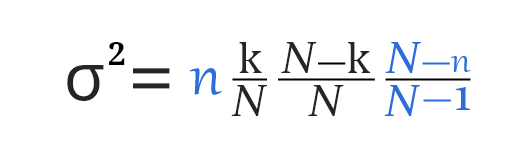
The variance of hypergeometric distribution can be calculated by using the following formula:
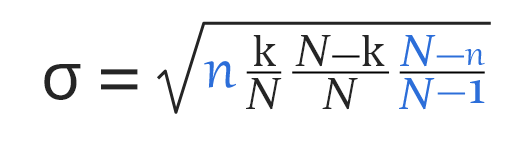
In this section, we’ll cover the step-by-step calculations of probability using the hypergeometric distribution.
Example 1:
Calculate the values of hypergeometric distribution if N = 54, K = 22, n = 17, and k = 7.
Solution:
Step 1: Calculate mean
μ = n * (K / N)
μ = 17 * 22 / 54
μ = 187/27
μ = 6.926
Step 2: Calculate variance:
σ2 = {n * (K / N)} * {(N - K) / N} * {(N - n) / (N - 1)}
σ2 = {17 * (22 / 54)} * {(54 - 22) / 54} * {(54 - 17) / (54 - 1)}
σ2 = 110704 / 38637
σ2 = 2.8652
Step 3: Calculate the probability:
P (X = 7) ≈ 0.233327502982322
P (X < 7) ≈ 0.402610817520716
P (X <= 7) ≈ 0.635938320503037
P (X > 7) ≈ 0.364061679496963
P (X >= 7) ≈ 0.597389182479284
Hypergeometric Distribution: Uses & Formula | Statistics by Jim.
Hypergeometric distribution| WallStreetMojo.
This report is generated by criticalvaluecalculator.com
Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.
