Give Feedback What do you think of quartile calculator?
Worst
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
Quartile calculator finds the order, interquartile range, first quartile, second quartile, and third quartile respectively of the entered data set.
The quartiles are the percentiles that divide the whole data into 4 equal parts, there are three types of quartiles.
Graphically, the quartiles can be displayed as:
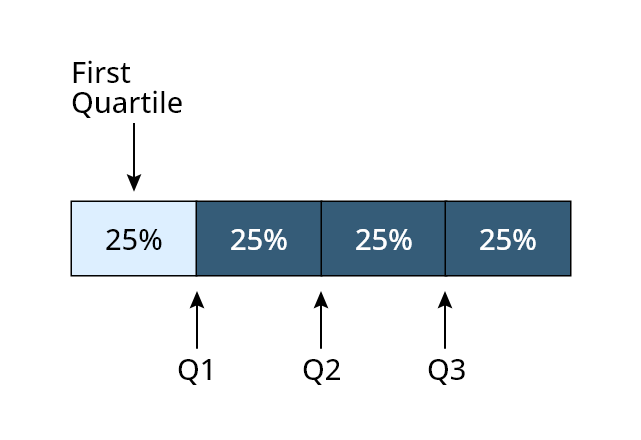
There are several formulas to calculate the quartiles of a data set, these are as follows:
Let “n” be the number of terms of a data set, then the quartiles can be given as
Q1 = {1(n +1)th / 4} term
Q2 = {2(n +1)th / 4} term
Q3 = {3(n +1)th / 4} term
IQR = Q3 – Q1
In the below examples, the method of finding quartiles is explained briefly.
Example 1:
Find Q1, Q2, Q3, and IQR of the set 9, 4, 5, 54, 76, 23, 95, 20, 74, 82, 9, 1.
Solution:
The data set is 9, 4, 5, 54, 76, 23, 95, 20, 74, 82, 1
Step 1: Arrange the data set in ascending order.
1, 4, 5, 9, 20, 23, 54, 74, 76, 82, 95
Step 2: Calculate the total number of terms “n”
Total terms = n = 11
Now calculate Q1, Q2, Q3, and IQR respectively.
For Q1:
The formula for Q1 is:
Q1 = {1(n +1) th / 4} term
Q1 = {1 (11+1) th / 4} term
Q1 = {(12) th / 4} term
Q1 = 3rd term
The 3rd term of the sequenced set is 5 so,
Q1 = 5
For Q2:
As Q2 is the median of the data set and the median is the central term of a sequenced set.
The set is 1, 4, 5, 9, 20, 23, 54, 74, 76, 82, 95
The central value is “23”
For Q3:
Q3 = {3(n +1) th / 4} term
Q3 = {3(11+1) th / 4} term
Q3 = {3(12) th / 4} term
Q3 = {(36) th / 4} term
Q3 = 9th term
9th term is 76 so,
Q3 = 76
For IQR:
IQR = Q3 – Q1
IQR = 76 – 5
IQR = 71
This report is generated by criticalvaluecalculator.com
Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.
