Median Calculator

Median Calculator

Median calculator is used to find the middle value of the data set. It calculates the median and ascending order in a fraction of a second.

What is the Median?

In central tendency, the median is the central number in the arranged set of data according to ascending or descending list of numbers. It is more descriptive of the data set than the mean.

Median is the 50% of the data set.

Formula of Median

The formula of the median is different for the even and odd numbers of data values (n).

When n is even

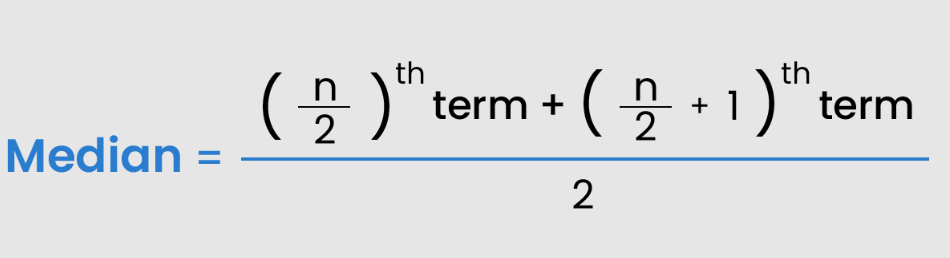
When n is odd

How to Calculate the Median?

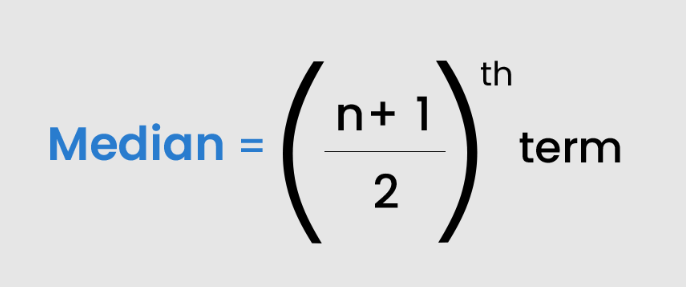
Here are a few examples of median to understand how to calculate it.

Example 1: For odd observations

Find the median of the given data set.

12, 34, 9, 6, 1, 4, 15

Solution

Step 1: Arrange the list of numbers in ascending order.

Ascending order = 1, 4, 6, 9, 12, 15, 34

Total observations = 7

Step 2: Now take the formula of the median.

Median = [(n+1)/2]^th term

Median = [(7+1)/2]^th term

Median = [8/2]^th term

Median = 4^th term

Hence, the median is the 4^th term of the ordered terms.

Step 3: Find the 4^th term of the ordered list.

9 is the 4^th term so,

Median = 9

Example 2: For even observations

Find the median of the given data set.

2, 14, 6, 12, 4, 10

Solution

Step 1: Arrange the list of numbers in ascending order.

Ascending order = 2, 4, 6, 10, 12, 14

Total observations = 6

Step 2: Now take the formula of the median.

Median = 1/2 [(n/2)^th + [n/2 + 1]^th]

Median = 1/2 [(6/2)^th + [6/2 + 1]^th]

Median = 1/2 [3^rd + [3 + 1]^th]

Median = 1/2 [3^rd + 4^th]

Step 3: Find the mean of the third and fourth terms of the sequence.

Median = 1/2 [6 + 12]

Median = 1/2 [18]

Median = 9

Frequently Asked Questions

1. What is n in the median formula?

In the median of a set of numbers, n represents the total number of observations or data points in the dataset.

2. Is medium difficult to calculate?

No, the median is the easiest statistical measure to calculate.

3. What is the use of the median? 

The median is used to measure a central tendency that is resistant to outliers and skewed data. It helps summarize the typical value in a dataset. It is useful for understanding distributions and comparing different datasets.