Give Feedback What do you think of mean absolute deviation calculator?
Worst
Poor
Average
Good
Excellent
Feedback Submitted Successfully.
Mean absolute deviation calculator is used to find the absolute deviation of the given set of data. This tool also provides sample size, mean, and absolute difference sum.
The mean absolute deviation of a dataset is the average distance between each data point and the mean. The idea of variability in a dataset can be taken from it.
The general formula of mean absolute deviation is:
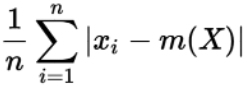
Below is a solved example of mean absolute deviation.
Example:
Find the mean absolute deviation of the given set of data
12, 14, 18, 24, 26, 32
Solution:
Step 1: Evaluate the mean.
Mean = x̅ = (12 + 14 + 18 + 24 + 26 + 32)/6
Mean = x̅ = 126/6
Mean = x̅ = 21
Step 2: Calculate the absolute deviation and add those deviations together.
| xi | xi - x̅ | | xi - x̅ | |
| 12 | 12 – 21 = -9 | |-9| = 9 |
| 14 | 14 – 21 = -7 | |-7| = 7 |
| 18 | 18 – 21 = -3 | |-3| = 3 |
| 24 | 24 – 21 = 3 | |3| = 3 |
| 26 | 26 – 21 = 5 | |5| = 5 |
| 32 | 32 – 21 = 11 | |11| = 11 |
| Σ| xi - x̅ | = 38 |
Step 3: To get the mean absolute deviation, divide the sum of the mean deviation by the total number of data values.
MAD = Σ| xi - x̅ | / n
MAD = 38/2
MAD = 19
Khan Academy. (n.d.). What is the mean absolute deviation? | Khan Academy
Formula & example of MAD | Study.com | Take Online Courses. Earn College Credit.
Criticalvaluecalculator.com is a free online service for students, researchers, and statisticians to find the critical values of t and z for right-tailed, left tailed, and two-tailed probability.
