Z Score Calculator

Find the z score of a statistical dataset using this z score calculator. It works with three different types of inputs:

• Data points
• Sample mean and size
• A sample data

It will calculate the z score for each value separately on inputting data points. For the other two inputs, the overall z-score is given. Z-Score table calculator gives the standard normal distribution graph. 

Z-score goes by the name normal score and standard score also. This is why this calculator is called a standard normal table calculator.

What is the Z-score?

Z-score is a statistical measure that helps evaluate the distance of each entry in a dataset from its mean value, expressed in terms of standard deviation. It allows us to understand how far away a particular value is from the sample's mean.

The Z-score calculation involves taking the difference between the value and the mean, and then dividing it by the standard deviation. A Z-score of 0 indicates that the value is equal to the mean, while a positive or negative Z-score indicates that the value is above or below the mean, respectively.

Think of standard deviation as a unit of measurement, similar to feet or inches, that provides context for the distances between individual data points and the mean.

Example:

For more clarity, Consider an example. Let’s say we calculated the standard deviation for a dataset and it was 10. Also, assume that its mean is 40.

We will make a scale of this data set like this:

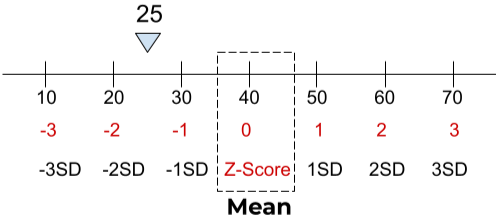
In this scale, every 10 units is equal to one standard deviation, as it was calculated. Now, let’s say one entry from the dataset is 25 and you want to find its z-score.

What will be its z-score? First, we know that 24 is smaller than 40, so the z-score is negative.

Next, it lies in the half of 20(-2 standard deviation) and 30 (-1 standard deviation). It is obvious that the point is -1.5 Standard deviations away from the mean.

Z-Score Formula

The z-score formula for data points

z = (x – µ)/σ 

The z-score formula for sample mean & size

z = (x̄ – µ)/ (σ/ √n)

The z-score formula for sample data

z = (x̄ – µ)/ (σ/ √n)

In the above equations,

• Z represents the z-score.
• x is the raw score or any dataset entry
• x̄ & μ represents the sample & population mean respectively.
• σ represents the population standard deviation
• n represents the total number of observations

How to find the z-score?

To find the z-score value, use the z-score probability calculator above. The manual method for finding the z-score is given below.

Example 1: For Sample Data

What are the z-score values for the following inputs?

• Sample data = [42, 54, 65, 47, 59, 40, 53]
• Population mean = 50
• Population Standard Deviation = 16

Solution:

Step 1: Count the entries.

n = 7

Step 2: Take the formula for finding the z-score from the sample set of data values.

z = (x̄ – µ)/ (σ/ √n)

Step 3: Find the sample mean.

x̄ = [42 + 54 + 65 + 47 + 59 + 40 + 53] / 7
    = 360 / 7
    = 51.4

Step 4: Put the values into the above formula.

z = (51.4 – 50)/ (16/√7)

z = (1.4)/(16/2.65)

z = (1.4)/(16/2.65)

z = 1.4/6.04

z = 0.2318

Example 2: For Data Points

What are the z-score values for the following inputs?

• Data points = 8
• Population mean = 20
• Population Standard Deviation = 10

Solution:

Step 1: Take the formula for finding the z-score from the data points.

z = (x – µ)/σ 

Step 2: Put the values to the above formula.

z = (8 – 20)/10

z = -12/10

z = -.12

Example 3: For sample mean and size

What are the z-score values for the following inputs?

• Sample mean = 19
• Sample size = 9
• Population mean = 15
• Population Standard Deviation = 12

Solution:

Step 1: Take the formula for finding the z-score from the sample set of data values.

z = (x̄ – µ)/ (σ/ √n)

Step 2: Put the values into the above formula.

z = (19 - 15) / (12/√9)

z = (4) / (12/3)

z = 4/4

z = 1